Pemograman Linear
Pemograman Linear
Pemrograman
Linier disingkat PL merupakan metode
matematik dalam mengalokasikan sumber daya yang terbatas untuk mencapai
suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya. PL banyak diterapkan dalam masalah ekonomi, industri,
militer, social dan lain-lain. PL berkaitan dengan penjelasan suatu kasus dalam
dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi
tujuan linier dengan beberapa kendala linier.
Contoh :
1. Seorang pengrajin menghasilkan satu tipe meja dan satu
tipe kursi. Proses yang dikerjakan hanya merakit meja dan kursi. Dibutuhkan
waktu 2 jam untuk merakit 1 unit meja dan 30 menit untuk merakit 1 unit kursi.
Perakitan dilakukan oleh 4 orang karyawan dengan waktu kerja 8 jam perhari.
Pelanggan pada umumnya membeli paling banyak 4 kursi untuk 1 meja. Oleh karena
itu pengrajin harus memproduksi kursi paling banyak empat kali jumlah meja.
Harga jual per unit meja adalah Rp 1,2 juta dan per unit kursi adalah Rp 500
ribu.
Formulasikan kasus tersebut ke dalam model matematiknya !
Jawab :
Solusi :Hal pertama yang harus dilakukan adalah
mengidentifikasi tujuan, alternatif keputusan dan sumber daya yang membatasi.
Berdasarkan informasi yang diberikan pada soal, tujuan yang ingin dicapai
adalah memaksimumkan pendapatan.
Alternatif keputusan adalah jumlah meja
dan kursi yang akan diproduksi. Sumber daya yang membatasi adalah waktu
kerja karyawan dan perbandingan jumlah kursi dan meja yang harus
diproduksi (pangsa pasar ).
Kita definisikan :
x1 = jumlah meja
yang akan diproduksi
x2 = jumlah kursi
yang akan diproduksi
Model umum Pemrograman Linier
kasus di atas adalah :
Fungsi tujuan :
Maksimumkan z = 1.2 x1
+ 0.5 x2
Kendala :
2x1 + 0.5 x2 ≤
32
x1/x2 ≥
¼ atau 4x1≥ x2 atau 4x1 – x2 ≥ 0
x1 , x2
≥ 0
2. Seorang peternak memiliki 200 kambing yang mengkonsumsi 90 kg pakan khusus
setiap harinya. Pakan tersebut disiapkan menggunakan campuran jagung dan
bungkil kedelai dengan komposisi sebagai berikut :
Bahan
|
Kg per kg bahan
|
|||
Kalsium
|
Protein
|
Serat
|
Biaya (Rp/kg)
|
|
Jagung
|
0.001
|
0.09
|
0.02
|
2000
|
Bungkil kedelai
|
0.002
|
0.60
|
0.06
|
5500
|
Kebutuhan pakan
kambing setiap harinya adalah paling banyak 1% kalsium, paling sedikit 30%
protein dan paling banyak 5% serat.
Formulasikan
permasalahan di atas kedalam model matematiknya !
Solusi :Hal pertama yang harus dilakukan adalah
mengidentifikasi tujuan , alternative keputusan dan sumber daya yang membatasi.
Berdasarkan informasi yang diberikan pada soal, tujuan yang ingin dicapai
adalah meminimumkan biaya pembelian
bahan pakan. Alternative keputusan adalah jumlah
jagung dan bungkil kedelai yang akan digunakan. Sumber daya yang membatasi
adalah kandungan kalsium, protein dan
serat pada jagung dan bungkil kedelai,
serta kebutuhan jumlah pakan per hari.
Kita definisikan :
x1 = jumlah jagung
yang akan digunakan
x2 = jumlah bungkil
kedelai yang akan digunakan
Model umum Pemrograman linier
kasus di atas oleh karenanya adalah :
Fungsi tujuan : minimumkan z =
2000 x1 + 5500 x2
Kendala :
x1 + x2
= 90
0.001 x1 + 0.002 x2
≤ 0.9
0.09 x1 + 0.6 x2
≥ 27
0.02 x1 + 0.06 x2
≤ 4.5
x1, x2 ≥
0
3.
Suatu bank kecil
mengalokasikan dana maksimum Rp 180 juta untuk pinjaman pribadi dan pembelian
mobil satu
bulan kedepan. Bank mengenakan biaya suku bunga per tahun 14% untuk pinjaman
pribadi dan 12% untuk pinjaman pembelian mobil. Kedua tipe pinjaman itu dikembalikan bersama dengan bunganya satu tahun
kemudian. Jumlah pinjaman pembelian mobil paling tidak dua kali lipat
dibandingkan pinjaman pribadi. Pengalaman sebelumnya menunjukkan bahwa 1% pinjaman
pribadi merupakan kredit macet.
Formulasikan masalah di atas
kedalam bentuk model matematiknya !
Solusi : Hal pertama yang harus
dilakukan adalah mengidentifikasi tujuan, alternatif keputusan dan sumber daya
yang membatasi. Berdasarkan informasi yang diberikan pada soal, tujuan yang
ingin dicapai adalah memaksimumkan pendapatan bunga dan pengembalian pinjaman.
Alternatif keputusan adalah jumlah alokasi
pinjaman pribadi dan pinjaman mobil. Sumber daya yang membatasi adalah jumlah alokasi anggaran untuk kredit bulan
depan dan perbandingan antara jumlah kredit pribadi dan pembelian mobil.
Kita definisikan :
x1 = jumlah anggaran
untuk pinjaman pribadi
x2 = jumlah anggaran untuk
pinjaman pembelian mobil.
Model umum Pemrograman Linier kasus
diatas adalah :
Fungsi tujuan : Maksimumkan z =
(0.14 – 0.01) x1 + 0.12 x2
Kendala :
x1 + x2 ≤ 180
x2 ≥ 2x1 atau
-2x1 + x2 ≥ 0
x1, x2 ≥ 0
4.
Suatu
pabrik perakitan radio menghasilkan dua tipe radio, yaitu HiFi-1 dan HiFi-2
pada fasilitas perakitan yang sama. Lini perakitan terdiri dari 3 stasiun
kerja. Waktu perakitan masing-masing tipe pada masing-masing stasiun kerja
adalah sebagai berikut :
Stasiun
kerja
|
Waktu perakitan per unit (menit)
|
|
HiFi-1
|
HiFi-2
|
|
1
|
6
|
4
|
2
|
5
|
5
|
3
|
4
|
6
|
Waktu kerja masing-masing stasiun kerja adalah 8 jam per
hari. Masing-masing stasiun kerja membutuhkan perawatan harian selama 10%, 14%
dan 12% dari total waktu kerja (8 jam) secara berturut-turut untuk stasiun
kerja 1,2 dan 3.
Formulasikan
permasalahan ini kedalam model matematiknya !
Solusi : Alternatif keputusan adalah : radio tipe HiFi-1 (x1) dan radio tipe HiFi-2 (x2). Tujuannya adalah memaksimumkan jumlah radio HiFi-1 dan
HiFi-2 yang diproduksi. Sumber daya pembatas adalah : jam kerja masing-masing stasiun kerja dikurangi dengan waktu yang dibutuhkan untuk
perawatan.
Waktu
produktif masing-masing stasiun kerja oleh karenanya adalah :
Stasiun
1 : 480 menit – 48 menit = 432 menit
Stasiun
2 : 480 menit – 67.2 menit = 412.8 menit
Stasiun
3 : 480 menit – 57.6 menit = 422.4 menit.
Model
umum pemrograman linier :
Maksimumkan
z = x1 + x2
Kendala
:
6x1
+ 4x2 ≤ 432
5x1
+ 5x2 ≤ 412.8
4x1
+ 6x2 ≤ 422.4
x1,
x2 ≥ 0
5.
Dua produk dihasilkan
menggunakan tiga mesin. Waktu masing-masing mesin yang digunakan untuk
menghasilkan kedua produk dibatasi hanya 10 jam per hari. Waktu produksi dan
keuntungan per unit masing-masing produk
ditunjukkan table di bawah ini :
Produk
|
Waktu produksi (menit)
|
|||
Mesin 1
|
Mesin 2
|
Mesin 3
|
Mesin 4
|
|
1
|
10
|
6
|
8
|
2
|
2
|
5
|
20
|
15
|
3
|
Formulasikan permasalahan di atas
ke dalam model matematiknya !
Solusi :
Alternatif keputusan adalah : produk 1 (x1) dan produk 2 (x2). Tujuannya adalah memaksimumkan keuntungan Sumber daya
pembatas adalah : jam kerja
masing-masing mesin.
Model umum pemrograman linier :
Maksimumkan z = 2x1 + 3x2
Kendala :
10 x1 + 5 x2 ≤
600
6 x1 + 20 x2
≤ 600
8 x1 + 15 x2
≤ 600
x1, x2 ≥ 0
6.
Empat produk diproses
secara berurutan pada 2 mesin. Waktu pemrosesan dalam jam per unit produk pada kedua
mesin ditunjukkan table di bawah ini :
Mesin
|
Waktu per unit (jam)
|
|||
Produk 1
|
Produk 2
|
Produk 3
|
Produk 4
|
|
1
|
2
|
3
|
4
|
2
|
2
|
3
|
2
|
1
|
2
|
Biaya
total untuk memproduksi setiap unit produk didasarkan secara langsung pada jam
mesin. Asumsikan biaya
operasional per jam mesin 1 dan 2 secara berturut-turut adalah $10 dan $5. Waktu yang disediakan
untuk memproduksi keempat produk pada mesin 1 adalah 500 jam dan mesin 2 adalah
380 jam. Harga jual per unit keempat produk secara berturut-turut adalah $65,
$70, $55 dan $45. Formulasikan
permasalahan di atas ke dalam model matematiknya !
Solusi
:
Alternatif
keputusan adalah : jumlah produk 1,2,3 dan 4 yang dihasilkan. Tujuannya adalah
memaksimumkan keuntungan. Perhatikan, keuntungan diperoleh dengan mengurangkan
biaya dari pendapatan.
Keuntungan
per unit dari produk 1 = 65 – (10x2 +
3x5) = 30
Keuntungan
per unit dari produk 2 = 70 – (10x3 + 2x5) = 30
Keuntungan
per unit dari produk 3 = 55 – (10x4 + 1x5) = 10
Keuntungan
per unit dari produk 4 = 45 – (10x2 + 2x5) = 15
Sumber
daya pembatas adalah waktu kerja yang disediakan kedua mesin.
Definisikan :
x1 : jumlah produk 1 yang dihasilkan
x2 : jumlah produk 2 yang dihasilkan
x3 : jumlah produk 3 yang dihasilkan
x4 : jumlah produk 4 yang dihasilkan
Model umum pemrograman linier :
Maksimumkan z = 30 x1 + 30x2 + 10 x3 + 15 x4
Kendala :
2x1 + 3 x2 + 4x3 + 2x4
≤ 500
3x1 + 2 x2 + x3 + 2x4
≤ 380
x1, x2, x3 , x4 ≥
0
- Suatu perusahaan manufaktur
menghentikan produksi salah satu produk yang
tidak menguntungkan. Penghentian ini menghasilkan kapasitas produksi yang
menganggur (berlebih). Kelebihan kapasitas produksi ini oleh manajemen
sedang dipertimbangkan untuk dialokasikan ke salah satu atau ke semua produk yang dihasilkan
(produk 1,2 dan 3). Kapasitas yang tersedia pada mesin yang mungkin akan
membatasi output diringkaskan pada table berikut :
Tipe mesin
|
Waktu yang dibutuhkan produk pada
masing-masing mesin (jam)
|
Waktu yang tersedia (jam per minggu)
|
||
Produk 1
|
Produk 2
|
Produk 3
|
||
Mesin milling
|
9
|
3
|
5
|
500
|
Lathe
|
5
|
4
|
0
|
350
|
Grinder
|
3
|
0
|
2
|
150
|
Bagian
penjualan mengindikasikan bahwa penjualan potensial untuk produk 1 dan 2 tidak
akan melebihi laju produksi maksimum dan penjualan potensial untuk produk 3
adalah 20 unit per minggu. Keuntungan
per unit masing-masing produk secara berturut-turut adalah $50, $20 dan $25.
Formulasikan
permasalahan diatas kedalam model matematik !
Solusi :
Alternatif keputusan :
Jumlah produk 1 yang dihasilkan = x1
Jumlah produk 2 yang dihasilkan = x2
Jumlah produk 3 yang dihasilkan = x3
Tujuannya adalah : memaksimumkan keuntungan Sumber daya
pembatas adalah :
Jam kerja mesin milling per minggu : 500 jam
Jam kerja mesin llathe per minggu : 350 jam
Jam kerja mesin grinder per minggu : 150 jam.
Model matematikanya adalah :
Maksimumkan z = 50 x1 + 20 x2 + 25 x3
Kendala :
9x1 + 3 x2 + 5x3 ≤ 500
5x1 + 4 x2 ≤ 350
3x1 + 2x3 ≤ 150
x3
≤ 20
x1,
x2, x3 g ≥ 0
Setelah kita dapat mendefinisikan soal permasalahan dalam bentuk model formula matematik barulah kita selesaikan masalah tersebut .
Kita ambil contoh nomor 5
Maksimumkan z = 2x1 + 3x2
Kendala :
10 x1 + 5 x2 ≤ 600
6 x1 + 20 x2 ≤ 600
8 x1 + 15 x2 ≤ 600
x1, x2 ≥ 0
1. Model Grafik
Persamaan I
x1 = 0 ==> 10 x1 + 5 x2 = 600 x2 = 0 ==> 10 x1 + 5 x2 = 600
x2 = 30 x1 = 100
Persamaan III
x1 = 0 ==>8 x1 + 15 x2 = 600 x2 = 0 ==> 8 x1 + 15 x2 = 600
15 x2 = 600 8 x1 = 600
x2 = 40 x1 = 75
Gambar Grafiknya :
Pers I dan II
10 x1 + 5 x2 = 600 x20 200 x1 + 100 x2 = 12000
6 x1 + 20 x2 = 600 x5 30 x1 + 100 x2 = 3000 -
170x1 = 9000
x1 = 52,9
10 x1 + 5 x2 = 600
10 (52,9) + 5 x2 = 600
5 x2 = 71
x2 = 14,2
Pers II dan III
6 x1 + 20 x2 = 600 x8 48 x1 + 160 x2 = 4800
8 x1 + 15 x2 = 600 x6 48 x1 + 90 x2 = 3600 -
70 x2 = 1200
x2 = 17, 14
6 x1 + 20 x2 = 600
6 x1 + 20(17,14) = 600
6 x1 = 257,2
x1 = 42,8
Dari tabel di atas didapatkan nilai max untuk x1 , x2 adalah ( 0 , 120 ) dengan nilai max 360

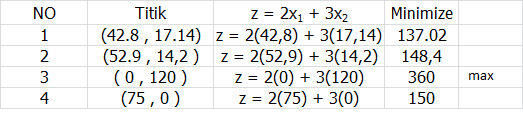


Komentar
Posting Komentar